Exponential EIP-1559

Exponential EIP-1559 explainer

In this blog post I will try to help understand how the exponential version of EIP-1559 works – the one that was suggested for the Shard Blob EIP.

I’m not going to try to explain how the EIP-1559 mechanism works – good explainers already exist, for example by Barnabé Monnot.

Linear EIP-1559 mechanics (“original version”)

I will call the current implementation of EIP-1559 the “linear version” of EIP-1559.

In the linear version, we define the constants

$$T = 15{,}000{,}000 \text{ (Gas target)}\\ A = 8 \text{ (Max base fee change denominator)}$$

Each block $B_i$ has a base fee of $b_i$ and total gas consumed in the block of $g_i$. There is an update rule for the Basefee:

$$b_{i+1} = b_i \cdot \left(1+ \frac{1}{A}\frac{g_i - T}{T}\right)$$

There is also a constraint that the maximum amoung of gas per block can’t be more than $2 T$. However, this limit is not important in the scope of this post so I will ignore it.

Exponential EIP-1559

One way to understand this “linear EIP-1559” better is to compute what happens after many updates. In particular, how does $b_n$ depend on $b_0$? By substituting the equation into itself many times, we get

$$b_{n} = b_0 \prod_{i=0}^{n-1} \left(1+ \frac{1}{A}\frac{g_i - T}{T}\right)$$

Now let’s say that $A$ is a large number, so that all the terms of the form $\frac{1}{A}\frac{g_i - T}{T}$ are small? Let’s call $x_i = \frac{g_i - T}{T}$.

If we assume this, we can use an approximation: The exponential function $e^x \approx 1+x$ for small $x$. We use this approximation in the inverse to replace $1+\frac{x_i}{A} = e^{\frac{x_i}{A}}$ to get

$$b_{n} = b_0 \prod_{i=0}^{n-1} \left(1+ \frac{x_i}{A}\right) \approx b_0 \prod_{i=0}^{n-1} e^\frac{x_i}{A} = b_0 \exp\left(\frac{1}{A}\sum_{i=0}^{n-1}x_i\right)$$

For the last step, we have used the property that $e^x \cdot e^y = e^{x+y}$. Note that

$$\frac{1}{A}\sum_{i=0}^{n-1}x_i = \frac{1}{TA}\sum_{i=0}^{n-1}(g_i - T) = \frac{1}{TA}\left(\sum_{i=0}^{n-1}g_i - nT\right)$$

so we get this new formula for $b_n$

$$b_{n} = b_0 \exp\left(\frac{1}{TA}\left(\sum_{i=0}^{n-1}g_i - nT\right)\right)= b_0 \exp\left(\frac{1}{TA}\left(G_n - T_n\right)\right)$$

where we used $G_n = \sum_{i=0}^{n-1}g_i$ for the total gas used since block 0 and $T_n = nT$ the cumulative gas target.

This is the exponential form of EIP-1559. The only thing we need to keep track of to compute the basefee current $b_n$ is (1) the total gas used, which is $G_n = \sum_{i=0}^{n-1}g_i$, and the total gas target, which is represented by $T_n = nT$ (so it’s enough to just count the number of blocks).

Analyzing the exponential form

Here is a question I have heard many times about exponential EIP-1559: Isn’t the goal of EIP-1559 that in the long term, the total gas used $G_n$ equals to the gas target $T_n$?

And if so, if you evaluate the equation for $G_n = T_n$, the exponential becomes one and thus $b_n = b_0$. So if the target is achieved, then the basefee would always be $b_0$ (which is typically very low)?

Here I will explain why this is not the case. Let’s see how this happens in linear EIP-1559 first. Here is a very simple economic model: Let’s assume a there is a “fair price” for gas at price $p$. For simplicity assume that below $p$, demand is infinite: All blocks will be filled. Above $p$, blocks will be empty. And when the base fee is equal to $p$, then there will be exactly enough demand to fill the blocks to half.

So what will happen in this model in linear EIP-1559?

• We assume that the base fee starts of low with $b_0 < p$.
• Then there will be a number of $n_0$ blocks where the basefee is lower than $p$, which will be completely full by our assumption.
• When the basefee reaches $p$ at $n_0$, all futher blocks will be filled to target.

To keep things simple, say the max block size is exactly $2T$. Then how much gas has been used at any block $n>n_0$? It would be $G_n = 2 n_0 T + (n - n_0) T = n_0 T + n T = T_n + n_0 T$. So it is actually not exactly the target, despite the EIP-1559 mechanism now being in equilibrium.

What happened? Note that it is still correct to say that EIP-1559 will ensure $G_n \approx T_n$; for example, if you take the fraction $\frac{G_n}{T_n}$, it will tend to $1$ so in asymptotic notation we would write $G_n \sim T_n$.

But there is a constant difference between $G_n$ and $T_n$, which is the amount of gas that was needed to shift the basefee from $b_0$ to $p$.

More generally, the current difference between $G_n$ and $T_n$ is a constant determined by the current basefee. In the linear version, this is approximately true; in the exponential version, it is exactly true (it follows directly from the definition $b_{n} = b_0 \exp\left(\frac{1}{TA}\left(G_n - T_n\right)\right)$)

Graphical illustration

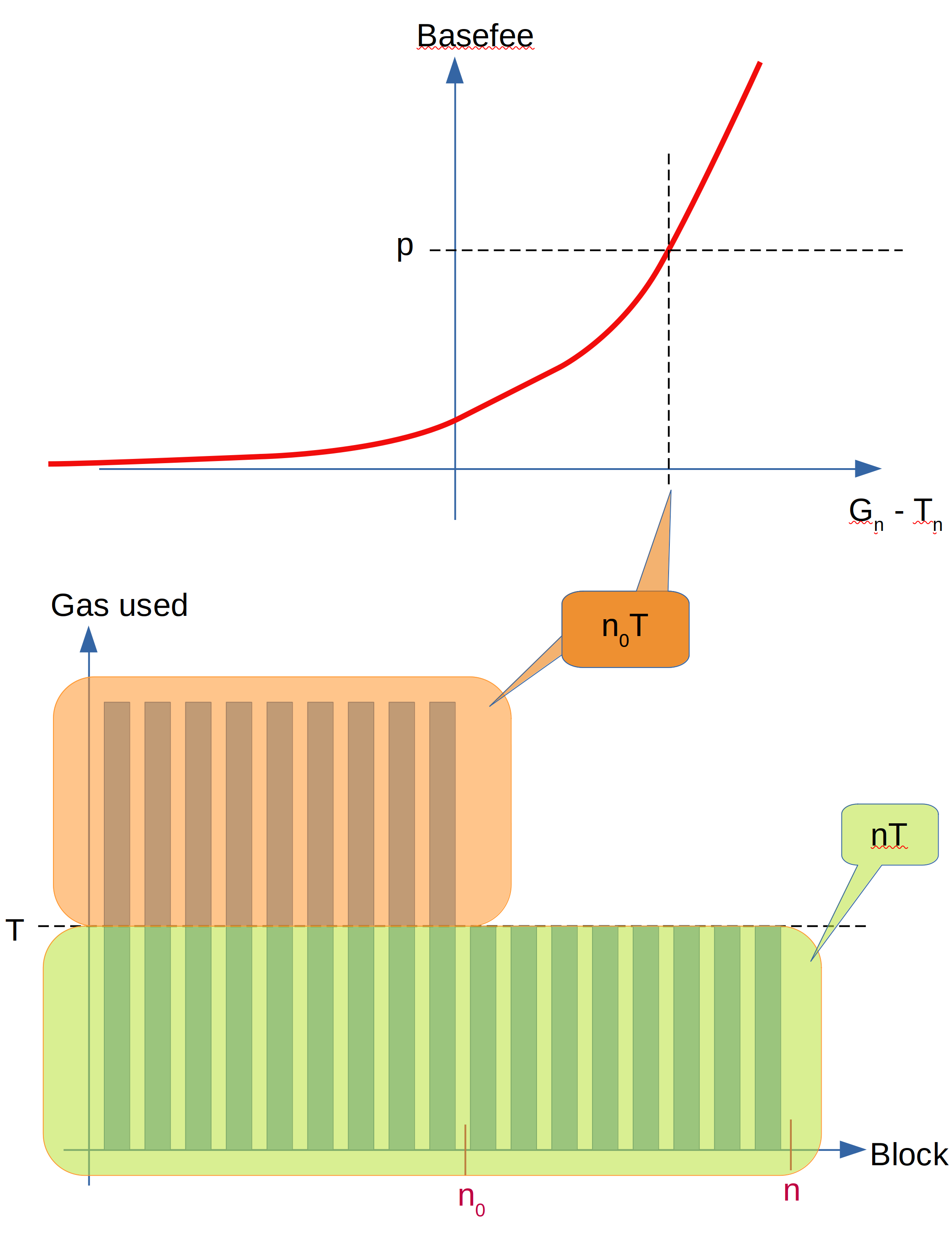
First let’s look at our simplified example. The following graph illustrates what is happening: Above you see the relation between total gas used and the basefee (an exponential function). Once in equilibrium, the basefee is at $p$ which means that $G_n-T_n = n_0 T$. Below we see how this adds up. The green shaded area of gas used is the blocks filled up to the target, and the orange area is the gas used above the target that sums up to $n_0 T$.

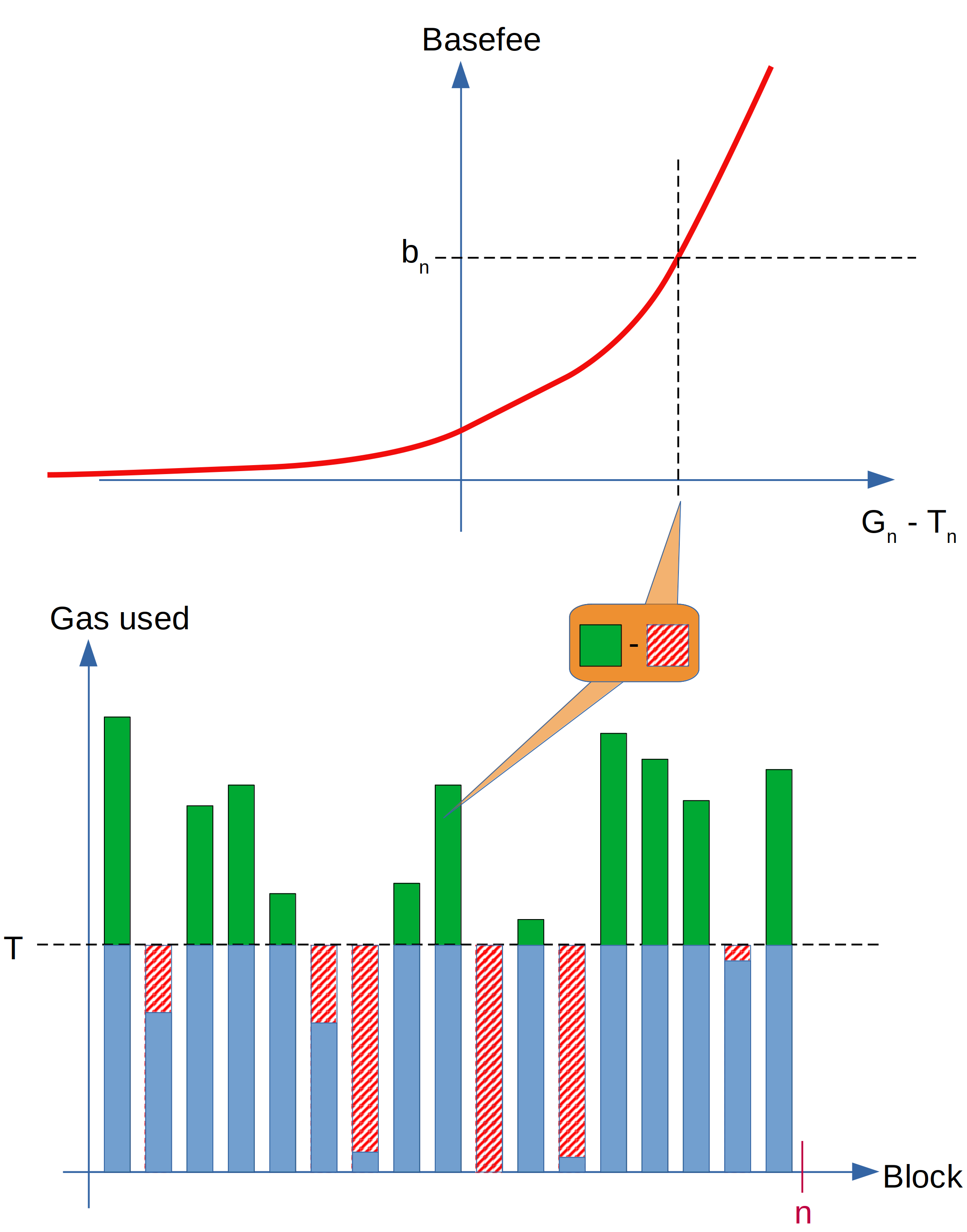
Next we look at a generic example, where some blocks are filled with more than target gas and some blocks are below. In this case, we need to sum up all the gas consumed by each block above the target (marked in green) and substract the gas that was below the target in underfull blocks (marked with red and white diagonal stripes). We can then read the sum on the $x$ axis of the basefee relation to determine the basefee $b_n$.

Appendix: Using differential equations to derive the exponential form

Here is another way of deriving the exponential form, using differential equations:

Let’s start from the update rule of linear EIP-1559

$$b_{i+1} = b_i \cdot \left(1+ \frac{1}{A}\frac{g_i - T}{T}\right)$$

We can rewrite this as

$$b_{i+1} - b_i = b_i \frac{1}{A}\frac{g_i - T}{T}$$

Tis is mathematically a difference equation. This is similar to a differential equation, but for finite differences. However, we can “approximate” it as a differential equation, by changing $i$ into a continuous variable and writing

$$b'(i) = b(i) \frac{1}{A}\frac{g(i) - T}{T}$$

where we use that $b(i)-b(i+1) \approx b'(i)$. You could say that this form comes about naturally if you assume that we are making the blocks smaller and smaller, scaling the target as well. As the size of the blocks goes towards zero, we get the differential equation.

This is a linear ordinary differential equation of first order that can be solved by moving the terms depending on $b$ to one side:

$$\frac{b'(i)}{b(i)} = \frac{1}{A}\frac{g(i) - T}{T}$$

Integrating on both sides yields:

$$\int\frac{b'(i)}{b(i)} = \ln b(i) = \int_{i=0}^n \frac{1}{A}\frac{g(i) - T}{T} + C$$

This is because

$$\frac{\mathrm{d}}{\mathrm{d}i} \ln b(i) = \frac{b'(i)}{b(i)}$$

So we can exponentiate and get

$$b(i) = \exp\left(\int_{i=0}^n \frac{1}{A}\frac{g(i) - T}{T} + C\right)$$

Since we want $b(0)=b_0$ we get $C=\ln b_0$ and so

$$b(i) = b_0\exp\left(\int_{i=0}^n \frac{1}{A}\frac{g(i) - T}{T}\right)$$

This looks almost the same that we derived above – except we now have an integral instead of a sum, because we are working with the continuous form.

The exponential version thus arises naturaly when you consider very small blocks and update the basefee each time. From this perspective, it is the most natural way of implementing EIP-1559.